Part Two: Music Theory: Equal Temperament, Notes, and Notation
This article will describe how the western musical scale is structured, using the Web Audio API.
window.audioContext = new (window.AudioContext || window.webkitAudioContext)();
Equal Temperament
If you live in the western world, your ears are most likely accustomed to the Twelve-Tone Equal Temperament (12-TET) system of tuning.
In this tuning, an octave is logarithmically divided into twelve semitones. An octave is simply the doubling of a frequency. Traditionally, the "A" above "middle C" (a specific note on a piano keyboard) is tuned to 440 Hz.
To calculate the frequency of some number of semitones from a reference tone, you can use the following formula:
freq = baseFreq × 2(numSemitones ÷ 12)
Or in javascript:
window.getFrequency = function (baseFreq, numSemitones) {
return baseFreq * Math.pow(Math.pow(2, 1/12), numSemitones);
};
Here's the code that made that form do its thing:
var gain = window.audioContext.createGain();
gain.gain.value = 0.5;
gain.connect(window.audioContext.destination);
var freqEl = document.querySelector('#tet .freq');
var baseFreqEl = document.querySelector('#tet .base');
var semitonesEl = document.querySelector('#tet .semitones');
var buttonEl = document.querySelector('#tet button');
function recalculate() {
var baseFreq = parseInt(baseFreqEl.value, 10);
var numSemitones = parseInt(semitonesEl.value, 10);
freqEl.value = getFrequency(baseFreq, numSemitones);
}
baseFreqEl.addEventListener('change', recalculate);
semitonesEl.addEventListener('change', recalculate);
recalculate();
buttonEl.addEventListener('click', function () {
var oscillator = audioContext.createOscillator();
oscillator.frequency.value = freqEl.value;
oscillator.connect(gain);
oscillator.noteOn(audioContext.currentTime + 0.00);
oscillator.noteOff(audioContext.currentTime + 1.00);
});
The Names of Notes
Since base frequencies and semitones are a pain to talk about, musicians use a notation to refer to specific reference frequencies. We use a letter (A through G, starting with C), a semitone modifier (♯ "sharp", ♭ "flat"), and an octave number (usually between 0 and 9). The octave number is incremented on each additional C note.
| Name | Semitones (relative to A) |
|---|---|
| C / B♯ | 3 |
| C♯ / D♭ | 4 |
| D | 5 |
| D♯ / E♭ | 6 |
| E / F♭ | 7 |
| F / E♯ | 8 |
| F♯ / G♭ | 9 |
| G | 10 |
| G♯ / A♭ | 11 |
| A | 0 |
| A♯ / B♭ | 1 |
| B / C♭ | 2 |
A4 is the fifth "A" key on a piano, and is usually tuned to be at exactly 440 Hz.
You may notice that A, D, and G are uniquely named (do not have neighbor notes that can reach them by adding a ♯ or ♭). This irregularity comes from the shape of the piano keyboard (which itself is due to the shape of the C Major scale)2. You can see that those are the only white keys surrounded by black keys on each side:
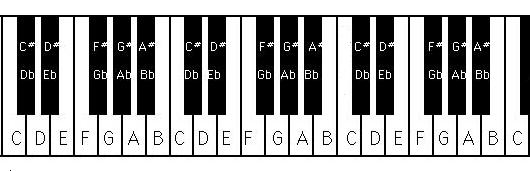
Each ♯ or ♭ added after the letter of the key acts as a modifier, meaning the key immediately to the right or the left, regardless of the color. We can now build a dictionary mapping this notation to the semitones relative to "A", and use the number of semitones to calculate the frequency of any named note:
var semitoneMap = {
C: 3,
D: 5,
E: 7,
F: 8,
G: 10,
A: 0,
B: 2
};
window.noteFrequency = function (name) {
var octaveIndex = (name.length === 3) ? 2 : 1;
var note = name[0];
var modifier = semitoneMap[note];
if (name[1] === '♯') {
modifier += 1;
} else if (name[1] === '♭') {
modifier += -1;
}
var octaveNumber = parseInt(name.substring(octaveIndex), 10);
if (note === 'A' || note === 'B') {
octaveNumber += 1;
}
var numSemitones = modifier + 12 * octaveNumber;
return getFrequency(440, numSemitones - (5 * 12));
};
Diatonic Scale
Although a 12-TET scale is broken into twelve distinct tones, not all of them are used in a phrase of music (usually). The combination of notes is very unpleasant, which can be successfully used to achieve a particular emotion in modern music, but is not usually found in most pieces. Instead, the most common set of notes is a division of the 12 notes into 7 distinct notes. This is called the diatonic scale.
We'll talk about this scale more when we discuss musical modes, but there are two main scales that come from the diatonic scale: the Major scale and the Minor scale.
| Diatonic Name | Major Scale | Minor Scale | ||
|---|---|---|---|---|
| Note | Semitones | Note | Semitones | |
| Tonic | C | 0 | C | 0 |
| Supertonic | D | 2 | D | 2 |
| Mediant | E | 4 | E♭ | 3 |
| Subdominant | F | 5 | F | 5 |
| Dominant | G | 7 | G | 7 |
| Submediant | A | 9 | A♭ | 8 |
| Leading Tone | B | 11 | B♭ | 10 |
| Tonic (Octave) | C | 12 | C | 12 |
The Major scale and Minor scale have distinct emotions associated with them, one is more happy and the other is more sad.
window.playNote = function (note, time, duration) {
var ctx = audioContext;
var osc = ctx.createOscillator();
osc.frequency.value = noteFrequency(note);
osc.connect(ctx.destination);
osc.noteOn(ctx.currentTime + time);
osc.noteOff(ctx.currentTime + time + duration);
return osc;
};
document.querySelector('.major-scale').addEventListener('click', function () {
var notes = ['C4', 'D4', 'E4', 'F4', 'G4', 'A4', 'B4', 'C5',
'B4', 'A4', 'G4', 'F4', 'E4', 'D4', 'C4'];
for (var i = 0; i < notes.length; ++i) {
playNote(notes[i], 0.15 * i, 0.15);
}
});
document.querySelector('.minor-scale').addEventListener('click', function () {
var notes = ['C4', 'D4', 'E♭4', 'F4', 'G4', 'A♭4', 'B♭4', 'C5',
'B♭4', 'A♭4', 'G4', 'F4', 'E♭4', 'D4', 'C4'];
for (var i = 0; i < notes.length; ++i) {
playNote(notes[i], 0.15 * i, 0.15);
}
});
Alternate Tunings
12-TET is not the only tuning that exists, it is historically derived from Just Intonation, which is the division of an octave into frequencies that match ratios of small numbers. To demonstrate the difference between the two, we can play a Major scale using Just Intonation and 12-TET:
| Diatonic Name | Semitones | 12-TET | Just Intonation |
|---|---|---|---|
| Tonic | 0 | 1.0 | 1/1 |
| Supertonic | 2 | 1.122462048309373 | 9/8 |
| Mediant | 4 | 1.2599210498948732 | 5/4 |
| Subdominant | 5 | 1.3348398541700344 | 4/3 |
| Dominant | 7 | 1.4983070768766815 | 3/2 |
| Submediant | 9 | 1.681792830507429 | 5/3 |
| Leading Tone | 11 | 1.8877486253633868 | 15/8 |
| Tonic (Octave) | 12 | 2.0 | 2/1 |
Creating an Interactive Piano Keyboard
Armed with the calculation of a note to a frequency, and a visual arrangement of a piano keyboard, we can construct a full, functional piano keyboard.
The code that handles the click events is here:
document.querySelector('.piano').addEventListener('click', function (evt) {
if (evt.target.hasAttribute('data-note')) {
var note = evt.target.getAttribute('data-note');
evt.target.classList.add('active');
playNote(note, 0, 0.5);
setTimeout(function () {
evt.target.classList.remove('active');
}, 500);
}
});
And the code that generates the actual piano DOM elements is here:
function makeKey(note) {
var key = document.createElement('div');
var container = document.createElement('div');
key.className = 'key';
container.appendChild(key);
container.className = (note[1] === '♭' || note[1] === '♯') ? 'black' : 'white';
key.setAttribute('data-note', note);
return container;
}
[].forEach.call(document.querySelectorAll('.piano'), function (piano) {
var keyContainer = document.createElement('div');
keyContainer.className = 'keys';
var keys = ['C', 'C♯', 'D', 'D♯', 'E', 'F', 'F♯', 'G', 'G♯', 'A', 'A♯', 'B'];
var aIndex = keys.indexOf('A');
var note;
for (var i = 0; i < 8; ++i) {
for (var j = (i === 0) ? aIndex : 0; j < keys.length; ++j) {
keyContainer.appendChild(makeKey(keys[j] + i));
}
}
keyContainer.appendChild(makeKey('C8'));
piano.appendChild(keyContainer);
});
In Conclusion
There is a strong mathematical relationship between the notation used to describe a particular frequency, and a strong physical relationship between the structure of the piano keyboard and the notation used to refer to particular keys. These relationships are very simple to programmatically describe, which helps us very quickly make an interactive piano keyboard.
In the next segment, we'll cover envelopes. Stay tuned!